Three years ago, I was asked to deliver the keynote address at the American Jewish Committee Annual Dinner. I chose to use that opportunity to explain what was so special about my childhood neighborhood, Squirrel Hill in Pittsburgh, Pennsylvania. After the attack in Squirrel Hill yesterday, just a short walk from the front door of … Continue reading Everything I Ever Needed to Know About Community, I Learned in the Shtetl of Squirrel Hill
Dialogue on Catalan Independence
Today the Parliament of Catalonia declared independence from Spain, a move Spain declares illegal. It is the first contested independence declaration in Western Europe since Sinn Fein declared the Irish Republic in 1919.(*) In an effort to understand the positions of both sides, I have created a dialogue between two imaginary characters, both Catalan. Gemma … Continue reading Dialogue on Catalan Independence
Intergenerational Mobility Isn’t Always a Good Thing
Over at Learn Liberty, I take on the recent kerfuffle over intergenerational mobility. Some scholars and journalists are saying that the U.S. has a major "problem" with mobility because its "churn" numbers (the rate at which children of rich parents fall into lower income deciles and children of poor parents rise into higher ones) are … Continue reading Intergenerational Mobility Isn’t Always a Good Thing
Federalism Isn’t Unfair
My latest for Learn Liberty looks at proposals for starting an equalization program to redistribute from rich to poor states in the U.S. and finds them wanting. Due to the audience for that blog, I kept that post nontechnical and brief. I'll reproduce part of it here and then elaborate on some of the complexities … Continue reading Federalism Isn’t Unfair
Should the U.S. Recognize Catalonia If It Secedes from Spain?
Over at Learn Liberty, I take up the question of what the rest of the world should do if Catalonia's referendum on independence on October 1 succeeds, as is expected. I apply some straightforward assumptions about justice and individual freedom to the case. Secession is hard because it always involves violating some people's rights -- … Continue reading Should the U.S. Recognize Catalonia If It Secedes from Spain?
What’s Wrong with Immigration Restrictions? The Same Thing That’s Wrong with Gun Control
My latest post at Learn Liberty explores the close parallels between certain arguments for immigration restrictions and gun restrictions: A common argument for restricting immigration to the United States and other developed countries — maybe even the most plausible one — runs like this. Opening the borders will bring in people who will consume more … Continue reading What’s Wrong with Immigration Restrictions? The Same Thing That’s Wrong with Gun Control
The Health Care Shell Game: Why Not Leave Policy to the States?
In my latest blog post for Learn Liberty, I take on arguments against decentralizing health care policy to the states on the grounds of fiscal capacity: So if federal ACA spending were cut or even zeroed out, why couldn’t states that like the legislation simply reinstate the same taxes and spending that the federal government … Continue reading The Health Care Shell Game: Why Not Leave Policy to the States?
Where Were the Libertarians in 2016?
In 2010 and 2015, I did some data analysis to see which states had the most libertarians, based on Libertarian Party and Ron Paul election results. I've now done something similar for 2016. Unfortunately, in 2016 we didn't have a libertarianish Republican presidential candidate continue through every primary, and so we can't use primary election … Continue reading Where Were the Libertarians in 2016?
Evaluating Pinker’s Claim That States Reduced War
Did the emergence of the state reduce the rate of human death from warfare? Steven Pinker's outstanding book, The Better Angels of Our Nature: Why Violence Has Declined, surveys many reasons why you are less likely to die from violence today than your ancestors were. Part of his explanation is that warfare was constant in … Continue reading Evaluating Pinker’s Claim That States Reduced War
Immanuel Kant, Philosopher of Freedom
My latest Learn Liberty blog post is on the topic above and can be found here. Excerpt: Kant’s moral philosophy justifies extremely strong individual rights against coercion. The only justification for coercion in his philosophy seems to be defense of self or others. His ideal government therefore seems to be extremely limited and to allow … Continue reading Immanuel Kant, Philosopher of Freedom
The Changing Political Geography of New Hampshire
Now that the 2016 election results are available by town for New Hampshire, I thought I would take a look at where libertarian candidates tended to do well or poorly, and how that pattern compared with conservative versus progressive support by town. To measure libertarian voting by town, I used different variables in different years. … Continue reading The Changing Political Geography of New Hampshire
Yes, Aaron Day Probably Cost Kelly Ayotte Re-Election
There's been some debate about whether independent conservatarian candidate Aaron Day (former chairman of the Free State Project Board of Directors) cost Republican Kelly Ayotte her U.S. Senate seat at this past election. Skeptics point to the fact that Day and Libertarian Brian Chabot between them about equaled Gary Johnson's vote percentage in the presidential … Continue reading Yes, Aaron Day Probably Cost Kelly Ayotte Re-Election
Can Government Spending Be Cut After All?
"What if we can't make government smaller?" the Niskanen Center's Will Wilkinson asks. He says that the evidence, particularly Wagner's Law, shows that government spending is impervious to political assault, and libertarians should make their peace with big government. Instead, libertarians should focus on reforming regulations to foster competition and the market process. I have … Continue reading Can Government Spending Be Cut After All?
Partisan Politics Makes Smart People Stupid
I've started a new blogging gig at Learn Liberty, a project of the Institute for Humane Studies. I'll be putting links to these posts here. My posts there will have the benefit of an editor, which is probably something I need. The first is on partisan rationalization and why epistocracy may not save us after … Continue reading Partisan Politics Makes Smart People Stupid
Happy Secession Day! Why N.H. Secession from the U.K. Was Awesome and Totally Justified
On this day, we celebrate other North American states' following New Hampshire's lead and declaring independence from the United Kingdom. Contrary to the contrarians, New Hampshire secession from the U.K. was awesome and totally justified for several reasons, to wit: New Hampshire abolished slavery in its 1785 constitution, 51 years before the U.K. followed suit. … Continue reading Happy Secession Day! Why N.H. Secession from the U.K. Was Awesome and Totally Justified
My Testimony on National Self-Determination Movements to the House Foreign Affairs Subcommittee on Europe, Eurasia, and Emerging Threats
On March 15, I had the opportunity to testify at the U.S. House Foreign Affairs Subcommittee on Europe, Eurasia, and Emerging Threats, chaired by California Rep. Dana Rohrabacher, on the topic of whether the U.S. government should change its policy toward national self-determination movements. I'm posting here my written testimony (my oral testimony had to … Continue reading My Testimony on National Self-Determination Movements to the House Foreign Affairs Subcommittee on Europe, Eurasia, and Emerging Threats
Research Questions for Economics Graduate Students
Are you an economics graduate student casting about for dissertation topics? I have a few ideas for you. As part of the rewriting of Freedom in the 50 States, I've been reviewing the economic literature on how various public policies affect consumer and producer surplus, deadweight loss, and so on. We use an estimate of … Continue reading Research Questions for Economics Graduate Students
In Which I Lose a Bet
Last year, I offered a bet that if an election were held this year in Catalonia, Catalan independentist parties would win a majority of valid, nonblank votes. One was, and they didn't. The only person to take me up on the bet was Bernat Gispert, who bet me dinner next time I'm in Barcelona, hoping … Continue reading In Which I Lose a Bet
Why Catalan Independence Might Be Good for the World
On September 27, Catalonia, an "autonomous community" of Spain, votes in a regional election that will likely determine whether the region declares independence from Spain. The Economist and other global news outlets have generally not taken the movement very seriously, which is a grave mistake. According to a series of new polls, the independentists are … Continue reading Why Catalan Independence Might Be Good for the World
Why Has Catalonia’s Independence Movement Lost Steam?
I don't blog much here anymore, in part because I've been too busy with Ethics & Economics Education, and in part because I find it easier to share quick thoughts on Twitter. Here's a little tweetstorm I had recently on Catalonia's independence vote next month: We might get crossover between Podemos & Ciudadanos soon. https://t.co/uiRhOp02gL— … Continue reading Why Has Catalonia’s Independence Movement Lost Steam?
How Decentralized Is Your State?
In the U.S., states have full authority over local government. Some states strictly centralize power and leave local government little to do. For instance, Hawaii has a single school district for the entire state, so that different localities cannot choose to spend different amounts on the government schools. Michigan effectively has a similar system, because … Continue reading How Decentralized Is Your State?
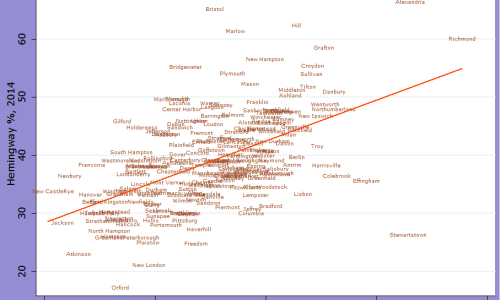
The Most and Least Libertarian Towns in New Hampshire (updated)
Updated to include two scatter plots Having examined which states have the most and least libertarians, I've decided to do something similar for the 239 populated towns of New Hampshire. Towns are the most important level of local government here, and therefore the degree of libertarian-ness should make some difference to policy at the town … Continue reading The Most and Least Libertarian Towns in New Hampshire (updated)
Where the Libertarians Are, Part 2
A few years ago, I did a statistical analysis of which states had the most libertarians, using data from 2004 and 2008 Libertarian Party vote shares and 2008 Ron Paul vote shares and contributions. David Boaz has prodded me to update these numbers in light of the 2012 election. This post does just that. To … Continue reading Where the Libertarians Are, Part 2
Talking with High School Students About Open Borders
New at e3ne.org, I discuss my conversations with high school students about the moral legitimacy of border restrictions: We started our discussion with a little bit of improv theatre. I played a foreigner trying to get into the United States without documentation. Students volunteered to play a border guard trying to keep me out. Between … Continue reading Talking with High School Students About Open Borders
Is the U.S. Government Illegitimate?
How can one group of human beings come to enjoy a right to enforce its authoritative commands on other human beings? In other words, how does government come to enjoy a right to rule, and how do citizens come to incur a duty to obey? I consider the answer over at e3ne.org. The reasoning depends … Continue reading Is the U.S. Government Illegitimate?
Is Poverty like a Pond?
New at e3ne.org, I take up Peter Singer's argument that we in affluent societies have far-reaching duties to aid the global poor, possibly to the extent of bringing ourselves down almost to their level. Excerpt: Instead of buying a Starbucks coffee once a week, you could save that money – about $200 over the course … Continue reading Is Poverty like a Pond?
The Meaning of the Arrow Theorem
Recently I finished reading the book Gaming the Vote by William Poundstone. I also assigned part of it to my Ethics & Economics Challenge students. It's a fun and informative read, draping heavy-duty political science in engaging story-telling. (My post at e3ne.org on the topic is here.) The book's central thesis is that the American … Continue reading The Meaning of the Arrow Theorem
Property Rights: Necessary but Not Sufficient for Prosperity
At e3ne.org, I have posted some reflections on my last discussion with the Ethics & Economics Challenge students, on the topic of private property rights. The work of Acemoglu, Johnson, and Robinson on how property rights support high levels of development plays a prominent role. Here's a scatter plot from their famous 2001 paper: Economies … Continue reading Property Rights: Necessary but Not Sufficient for Prosperity
The Miracle of the Price System
This week's post at e3ne.org is about the miracle of the price system: Natural disasters harm people’s standard of living by destroying resources, but in a free marketplace, rising prices and profits in scarce goods give both buyers and sellers an incentive to heal the economic wound. Drawn by the possibility of making good profits … Continue reading The Miracle of the Price System
Do You Really Understand Comparative Advantage?
The theory of comparative advantage shows how voluntary exchange benefits both parties and encourages specialization. You don't need to possess an absolute advantage in any particular productive activity to enjoy a comparative advantage. Your comparative advantage is whatever you can do relatively cheaply compared to everything else and everyone else. For instance, Haiti still trades … Continue reading Do You Really Understand Comparative Advantage?
What “Buy Local” Campaigns Get Wrong
The economic thinking behind "buy local" campaigns is typically terrible. One such example is the claim that a dollar "circulates more" when you spend it locally. The rate of circulation of a dollar doesn't create any wealth. Try it out: circulate a dollar among a group of friends and feel your standard of living stay … Continue reading What “Buy Local” Campaigns Get Wrong
Mill on Paternalism
I have a "nutshell" summary and critique of John Stuart Mill's On Liberty now up at e3ne.org. Excerpt: Mill thus defends freedom of conscience, speech, and lifestyle on completely “practical” grounds, but he leaves some significant loose ends in On Liberty. For instance, there are lots of examples of “harms” that the government shouldn’t regulate, … Continue reading Mill on Paternalism
FDI & Civil Conflict
How does globalisation, especially foreign direct investment, influence the risk of intrastate conflict? While several prominent studies have found that globalisation reduces the probability of civil war, we use new data and methods to approach the question. In particular, we test for the possibility that foreign investment is endogenous to conflict risk and appropriately use … Continue reading FDI & Civil Conflict
A Right to Do Wrong?
The latest in my series of blog posts based on discussions with Ethics & Economics Challenge students is up at e3ne.org. It's on whether it's possible for us to have a right to do wrong in some cases, i.e., for there to be some moral obligations that it is not morally permissible to enforce. A … Continue reading A Right to Do Wrong?
Adam Smith on Beneficence & Justice
I've recently begun the Ethics & Economics Challenge program with students at Merrimack Valley High School in Concord, N.H. We've been discussing what Adam Smith's Theory of Moral Sentiments can tell us about what types of moral duties may legitimately be enforced. I'm blogging my reflections as we go. Here is a selection from the … Continue reading Adam Smith on Beneficence & Justice
The Eight Year Mirage
The search for a legacy always begins in earnest as presidents approach the final years of their time in office. Josh Kraushaar (National Journal) has an interesting piece on the Obama legacy. A key passage: By ignoring the electorate and steering the country in an unmistakably progressive direction his final two years in office, he's … Continue reading The Eight Year Mirage
The Reformicons
Thomas B. Edsall has an interesting piece in the New York Times on the “Republican Discovery of the Poor,” the embrace of economic populism, and the promotion of reforms, including changes to the tax code. Edsall understands the potential challenge to Democrats as Republicans “plan to bring the fight to the Democrats on their own … Continue reading The Reformicons
Does Moral Action Depend on Reasoning?
Just came across this Templeton Foundation conversation on the role of reason in moral thought and action. Very enlightening. Over time, I have become more of a "Smithian" in acknowledging the role of moral emotion in guiding our intuitions and appropriately establishing moral commitments, though I also see a role for reason in systematizing those … Continue reading Does Moral Action Depend on Reasoning?
Libertines, Hypocrites, and the Weak-Willed, With an Application to Socialism
Bryan Caplan argues that social conservatives should prefer libertines to hypocrites, contrary to the common meme that "at least hypocrites have moral standards." The argument is pretty simple: hypocrites seem to share your values, but when you least expect it, they will betray you. So far as it goes, the argument is pretty convincing. But … Continue reading Libertines, Hypocrites, and the Weak-Willed, With an Application to Socialism
The Big Chill
Despite candidate Obama’s promises of greater openness and transparency, the last few years have not been good ones with respect to freedom of the press. As Al Hunt observes: “The Obama administration has pursued more journalists than other administrations, secretly looking at phone records and credit card transactions and surreptitiously tracking their movements.” A new … Continue reading The Big Chill